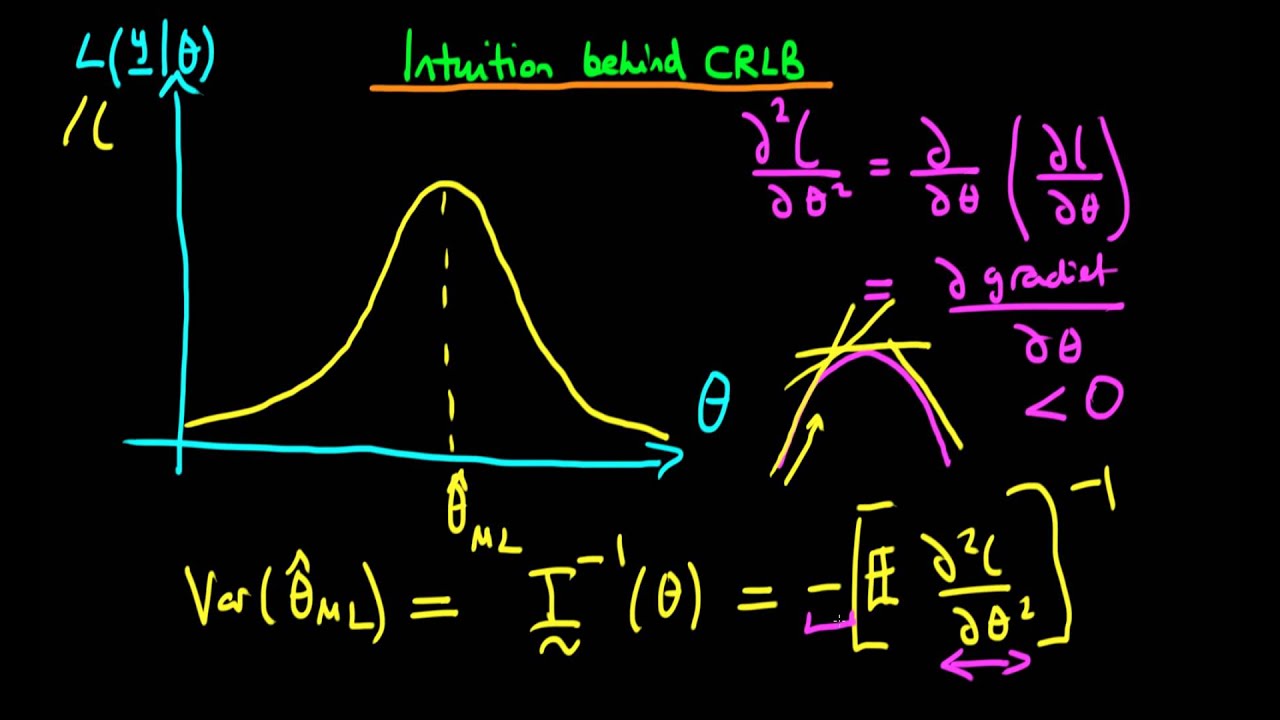
Imagine an archer aiming at a target: the sharpness of the arrow determines how closely it can hit the bullseye. The Cramér-Rao Bound is like the sharpness of an estimator—it defines the theoretical lower limit of variance for an unbiased estimate. By understanding this bound, analysts can ensure their statistical and machine learning models achieve optimal precision.
A Brief History of the Cramér-Rao Bound
Developed in the 1940s by statisticians Harald Cramér and Calyampudi Radhakrishna Rao, the Cramér-Rao Bound transformed the field of estimation theory. This mathematical framework provided a way to measure the precision of statistical estimators. Today, it is widely used in machine learning, signal processing, and econometrics, helping researchers and engineers assess the efficiency of their models.
What Is the Cramér-Rao Bound?
The Cramér-Rao Bound defines the minimum variance an unbiased estimator can achieve for a given parameter. It acts as a benchmark, highlighting how close an estimator comes to the theoretical limit of accuracy.
Key features:
- Applies to unbiased estimators, where the expected value equals the true parameter.
- Provides a reference to evaluate estimator efficiency and precision.
In the archer metaphor, the bound represents the arrow’s sharpness: regardless of the archer’s skill, the arrow’s sharpness sets the limit on accuracy.
Why Is the Cramér-Rao Bound Important?
The Cramér-Rao Bound addresses key challenges in statistical estimation:
- Efficiency: Determines whether an estimator achieves the optimal level of precision.
- Benchmarking: Compares the performance of different estimators.
- Error Minimization: Guides the development of methods to reduce variance while maintaining accuracy.
For example, in healthcare analytics, applying the Cramér-Rao Bound ensures precise estimates of disease prevalence, enabling policymakers to allocate resources effectively.
How Is the Cramér-Rao Bound Used?
The bound relies on the Fisher Information, a measure of the information content in the data regarding the parameter being estimated. Steps include:
- Deriving the Fisher Information from the probability distribution of the data.
- Calculating the Cramér-Rao Bound to determine the minimum variance.
- Evaluating whether an estimator achieves this variance to confirm its efficiency.
In signal processing, this approach is critical for accurate frequency estimation, ensuring robust communication systems.
Applications of the Cramér-Rao Bound
- Parameter Estimation: Used in econometrics, machine learning, and physics to evaluate estimator performance.
- Signal Processing: Ensures precision in signal reconstruction and filter design.
- Statistical Testing: Provides benchmarks for assessing the reliability of statistical methods.
Categories of Estimators
- Efficient Estimators: Achieve the minimum variance specified by the Cramér-Rao Bound.
- Inefficient Estimators: Have higher variance than the bound, indicating the potential for optimization.
Software and Tools for the Cramér-Rao Bound
- Python Libraries:
- Scipy.stats: Offers tools for Fisher Information and efficiency evaluations.
- Statsmodels: Provides variance analysis and benchmarking functions.
- MATLAB: Advanced visualization and analysis tools for deriving the Cramér-Rao Bound in signal processing.
- R Programming: Packages like MASS and infer support estimation and efficiency analysis.
Industry Applications in Australian Governmental Agencies
- Healthcare Analytics: The Australian Institute of Health and Welfare uses the Cramér-Rao Bound to improve disease prevalence models, ensuring effective resource distribution.
- Environmental Monitoring: Geoscience Australia applies the bound to satellite data analysis, optimizing estimates for land use and environmental changes.
- Public Transport Planning: Transport for NSW incorporates the bound in traffic flow models, refining predictions and enhancing resource allocation.
