A Very Short Introduction of Manifold Assumption

A Brief History: Who Developed the Manifold Assumption?

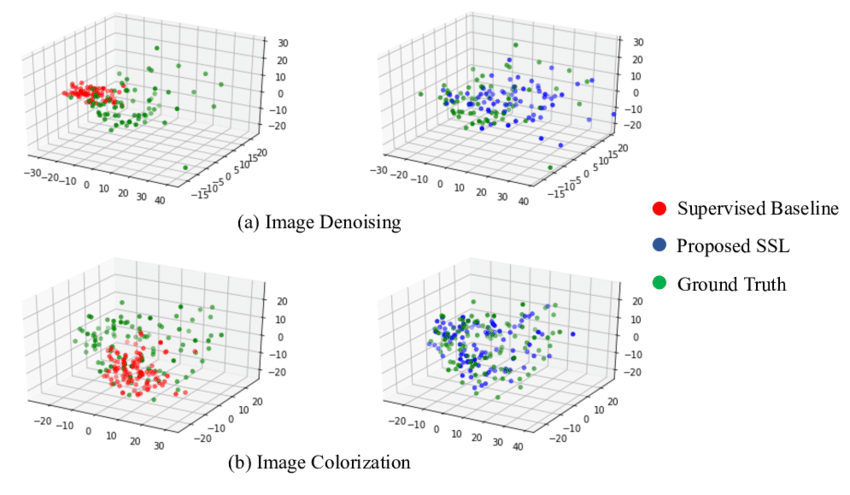
The manifold assumption, a foundational concept in semi-supervised learning (SSL), became widely recognized in the late 1990s and early 2000s. Researchers like Sam Roweis, Lawrence Saul, and Joshua Tenenbaum contributed to its development through dimensionality reduction and nonlinear mapping techniques. The assumption underpins key methods like t-SNE, Isomap, and Laplacian Eigenmaps, which are essential for data visualization and machine learning workflows.

What Is the Manifold Assumption?

The manifold assumption posits that high-dimensional data often resides on a low-dimensional manifold within the feature space. This simplification allows machine learning models to identify meaningful structures while ignoring noise.

Imagine navigating a winding path through a dense forest: the path represents the manifold, guiding the way through complex, high-dimensional data. Models trained with this assumption focus only on relevant paths, improving accuracy and reducing complexity.

Why Is It Used? What Challenges Does It Address?

The manifold assumption addresses key challenges in semi-supervised learning:

• Dimensionality Reduction: Simplifies high-dimensional data by mapping it to essential structures.
• Improved Generalization: Helps models focus on intrinsic data patterns, improving performance on unseen data.
• Efficient Learning: Reduces computational requirements while maintaining accuracy.

Without the manifold assumption, models risk overfitting to noisy, irrelevant features, leading to inefficiency and poor predictions.

How Is It Used?

1. Dimensionality Reduction: Apply techniques like t-SNE or Isomap to identify low-dimensional manifolds.
2. Model Training: Train models on the reduced feature space to enhance focus and efficiency.
3. Semi-Supervised Techniques: Use methods like label propagation to extend labels to unlabeled data along the manifold.

Different Types of Manifold Assumptions

1. Linear Manifolds: Assume data resides on a flat, low-dimensional plane (e.g., Principal Component Analysis, PCA).
2. Nonlinear Manifolds: Model curved, intricate structures in data, using algorithms such as t-SNE or Isomap.

6. Key Features

• Intrinsic Data Focus: Captures the underlying structure of data for better generalization.
• Dimensionality Reduction: Simplifies data representation while retaining critical information.
• Improved Accuracy: Removes noise, enabling models to focus on relevant features.

Software and Tools Supporting the Manifold Assumption

• Python Libraries:
  • Scikit-learn: Offers tools like t-SNE, Isomap, and Locally Linear Embedding (LLE).
  • TensorFlowand PyTorch: Enable integration of manifold learning in machine learning workflows.
  • FastAI: Simplifies workflows with support for dimensionality reduction techniques.
• Platforms: Tools like Google Colab and Jupyter Notebooks facilitate interactive experimentation with manifold learning methods.

3 Industry Application Examples in Australian Governmental Agencies

1. Healthcare (Department of Health):
   • Application: Analyzing patient data for disease detection.
   • Use of Manifold Assumption: Reduces complex health metrics into interpretable, low-dimensional patterns.
2. Environmental Management (Department of Agriculture, Water, and the Environment):
   • Application: Classifying ecosystems based on satellite imagery.
   • Use of Manifold Assumption: Maps environmental data to low-dimensional spaces, simplifying analysis.
3. Transportation (Department of Infrastructure, Transport, and Regional Development):
   • Application: Predicting traffic congestion trends.
   • Use of Manifold Assumption: Identifies meaningful patterns in traffic data through dimensionality reduction.