A Brief History: Who Developed the Huber Cost Function?
The Huber cost function, also known as Huber loss, was introduced by Peter J. Huber in 1964. Huber, a Swiss statistician, developed this function to create a robust method for regression analysis that is less affected by outliers and extreme values than traditional squared error loss functions.
What Is the Huber Cost Function?
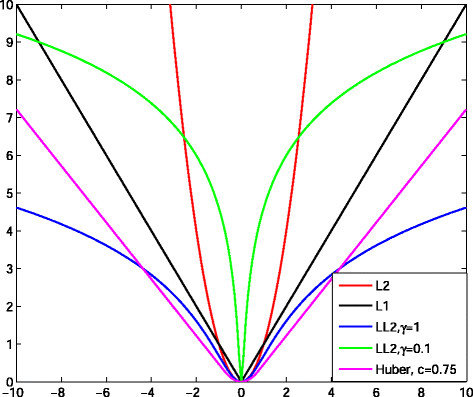
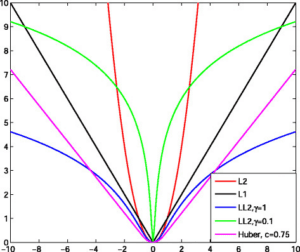
The Huber cost function is a loss function used in machine learning, particularly in regression tasks. It combines the best of both worlds from Mean Squared Error (MSE) and Mean Absolute Error (MAE): providing a balance between sensitivity to small errors and robustness to outliers.
It works like a hybrid suspension system. On smooth roads (small errors), it glides effortlessly, like MSE handling minor discrepancies well. When hitting a pothole (an outlier), the sturdy suspension (MAE) softens the impact, preventing damage.
Why Is It Used? What Challenges Does It Address?
The Huber cost function addresses the challenge of outliers in data. In many datasets, extreme values can skew results and degrade the performance of models using traditional loss functions like MSE.
- Robustness to Outliers: Reduces the impact of outliers, leading to more reliable machine learning models.
- Balanced Error Measurement: A compromise between squaring errors (which exaggerates outliers) and taking their absolute value (which can ignore small errors).
Without the Huber cost function, models might fail to handle the challenges of real-world data.
How Is It Used?
The process involves three steps:
- The model predicts an outcome.
- The Huber function evaluates the error.
- Optimization algorithms adjust the model to minimize the error.
This iterative process improves model performance over time, much like refining a skill through practice.
Different Types
- Pseudo-Huber Loss: A smooth approximation of the Huber loss that is differentiable everywhere, which can be useful for specific optimization algorithms.
- Adaptive Huber Loss: Dynamically adjusts the delta parameter based on the data distribution.
Different Features
- Delta Parameter: Controls the sensitivity to outliers.
- Differentiability: Smooth transition between MSE and MAE enables efficient optimization.
- Versatility: Suitable for various regression tasks where data may contain outliers.
Software and Tools Supporting the Huber Cost Function
- Python Libraries:
- TensorFlow: Use tf.keras.losses.Huber() for Huber loss implementation.
- PyTorch: Use torch.nn.SmoothL1Loss() for equivalent functionality.
- Scikit-learn: Offers robust regression models leveraging the Huber loss.
- Platforms: Jupyter Notebooks and Google Colab for experimentation and implementation.
Industry Application Examples in Australian Governmental Agencies
- Environmental Monitoring: Predicting pollution levels where sensor errors occur.
- Use of Huber Loss: Mitigates the impact of faulty readings on predictive models.
- Transportation Planning: Estimating traffic flow and congestion levels.
- Use of Huber Loss: Handles anomalies in traffic data due to accidents or special events.
- Public Health Analysis: Modeling disease outbreak patterns where sudden spikes occur.
- Use of Huber Loss: Reduces the influence of outliers in health data, improving resource allocation.
How interested are you in uncovering even more about this topic? Our next article dives deeper into [insert next topic], unravelling insights you won’t want to miss. Stay curious and take the next step with us!