Hidden Markov Models: Revolutionising Sequential Data Analysis
Hidden Markov Models (HMMs), first introduced in the 1960s by Leonard E. Baum and colleagues, have transformed the analysis of sequential data. By the 1980s, advancements in computational power elevated HMMs to essential tools across fields like speech recognition, bioinformatics, and natural language processing.
What Are Hidden Markov Models? A Peek Behind the Mechanisms
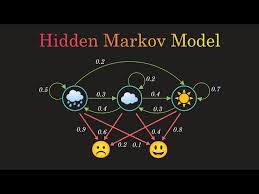
HMMs operate like the gears inside a clock: while the observable emissions are akin to the visible movement of the clock hands, the hidden states represent the internal mechanisms driving those movements. By piecing together clues from the visible outputs, HMMs help uncover the full operation of the system.

Why Use HMMs? Solving Temporal and Sequential Data Challenges
HMMs excel in decoding complex sequential data by addressing key challenges:
- Temporal Data Modelling: Understanding time-dependent sequences.
- Interpreting Incomplete Observations: Making sense of missing or partial data.
- Cross-Domain Applications: Tackling problems in healthcare, finance, and communication systems.
How Hidden Markov Models Work: A Step-by-Step Guide
Using HMMs involves several steps, similar to assembling a puzzle with missing pieces:
- Define Hidden States and Emissions: Identify concealed mechanisms (hidden states) and their observable effects (emissions).
- Estimate Probabilities: Assign likelihoods to state transitions and observed outputs.
- Run Algorithms: Employ methods like the Forward-Backward or Viterbi algorithm to navigate the puzzle and determine the most probable outcomes.
- Interpret Insights: Translate the results into actionable decisions or predictions.
Exploring HMM Variants: Discrete, Continuous, and Semi-Markov Models
HMMs come in various forms, each tailored to specific types of data:
- Discrete HMMs: Handle categorical emissions, like analog clocks showing specific hours.
- Continuous HMMs: Manage continuous emissions with precision, akin to digital clocks.
- Hidden Semi-Markov Models (HSMMs): Accommodate states with variable durations, perfect for irregular time intervals.
Features That Make HMMs Powerful for Data Analysis
HMMs possess unique features that make them indispensable for analysing sequential data:
- Markovian Property: Each state depends only on its immediate predecessor.
- Parameter Learning: Adjusts probabilities for optimal performance.
- Computational Efficiency: Quickly and accurately manages complex systems.
- Scalability: Adapts seamlessly to both small and large datasets.
Top Tools for HMM Development: Python, MATLAB, and More
Several advanced tools simplify the development and implementation of HMMs:
- Python (hmmlearn, PyTorch): Flexible and modular tools for HMM creation.
- MATLAB: Ideal for simulation and predictive modelling.
- R (depmixS4): Customisable analysis tools for researchers.
- H2O.ai: Efficiently processes large datasets for predictive analytics.
HMMs in Action: Applications Across Australian Government Agencies
HMMs play a critical role in enhancing operations across various Australian industries:
- Australian Taxation Office: Detects fraudulent activities by analysing transactional patterns.
- CSIRO: Deciphers genetic sequences and environmental data for improved research outcomes.
- Department of Transport: Models traffic flows to optimise urban transport networks.

Conclusion
Hidden Markov Models are a cornerstone of modern data analysis, enabling insights into sequential patterns across various domains. From traffic modelling to fraud detection, their adaptability and efficiency make them invaluable tools in Australian industries.
How interested are you in uncovering even more about this topic? Our next article dives deeper into [insert next topic], unravelling insights you won’t want to miss. Stay curious and take the next step with us!