A Very Short Introduction of Gaussian Mixture Models

The Evolution of Gaussian Mixture Models: From Theory to Application

The Gaussian Mixture Model (GMM) has its roots in statistical theory, originating with Karl Pearson in 1894. He introduced the concept of mixtures of distributions to analyse multimodal data. This foundation was later refined by Dempster, Laird, and Rubin in the 1970s with the Expectation-Maximisation (EM) algorithm, which provided a systematic way to estimate model parameters.

What Is a Gaussian Mixture Model? Simplifying Complex Data Clustering

Imagine a room filled with various types of fruit—apples, oranges, and bananas—all mixed together. A Gaussian Mixture Model acts like a sophisticated sorting machine that groups these fruits based on shared characteristics such as size, colour, or shape. It assumes data points are generated from several Gaussian distributions, each representing a distinct cluster.

Why Use GMM? Addressing Data Clustering Challenges

Gaussian Mixture Models are powerful tools in machine learning and data analysis because they:

• Cluster Data Without Labels: Useful for unsupervised learning.
• Estimate Density: Helps to model data distributions in complex spaces.
• Manage Overlapping Data: Assigns probabilities to data points rather than fixed labels.

These capabilities enable GMMs to tackle challenges such as:

• Handling Ambiguity: Probabilistic assignment of clusters minimises errors in classification.
• Adapting to Real-World Complexity: Effectively models overlapping or irregular data clusters.

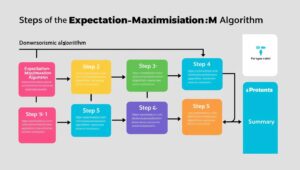
Gaussian Mixture Models Work: A Step-by-Step Guide

Gaussian Mixture Models follow a structured process:

1. Initialisation: Determine the number of Gaussian components (clusters).
2. Expectation-Maximisation (EM): Iteratively refine cluster probabilities and parameters such as mean and covariance.
3. Prediction: Classify data points into the most probable clusters based on learned probabilities.

Example: GMM can be used to analyse customer demographics and identify market segments for tailored marketing campaigns.

Exploring Types of GMMs: Diagonal, Full Covariance, and More

GMMs come in different forms to suit various data requirements:

1. Diagonal GMM: Uses diagonal covariance matrices, making it ideal for large datasets.
2. Full Covariance GMM: Captures intricate relationships between clusters with more parameters.
3. Tied Covariance GMM: Shares covariance matrices across clusters, simplifying computations.

Key Features That Make GMMs Indispensable

GMMs stand out due to their key features:

• Probabilistic Clustering: Assigns probabilities to each data point for every cluster.
• Flexible Data Modelling: Manages complex and overlapping data distributions.
• Scalability: Performs well with both small and large datasets.

Top Tools for GMM Implementation: Python, R, and MATLAB

Several tools and software make GMMs accessible for practitioners:

• Python Libraries: Scikit-learn, TensorFlow Probability, and PyTorch.
• R Packages: mclust for advanced clustering.
• MATLAB: Ideal for academic and industry-level research.

Real-World Applications of GMMs in Australian Government Agencies

GMMs are widely used across Australian government sectors for impactful results:

1. Healthcare Analytics:
   • Application: Clustering patient data for personalised treatment strategies.
   • Use of GMM: Groups patients based on health metrics for targeted interventions.
2. Traffic Flow Analysis:
   • Application: Segmenting traffic patterns for urban planning.
   • Use of GMM: Identifies high-congestion areas to optimise traffic management strategies.
3. Environmental Monitoring:
   • Application: Analysing data trends for resource management.
   • Use of GMM: Models climate data to predict changes and allocate resources effectively.

Conclusion

Gaussian Mixture Models are a cornerstone of machine learning, offering robust solutions for clustering and density estimation. Their adaptability and efficiency make them essential tools in fields like healthcare, urban planning, and environmental monitoring. With the support of advanced software and ongoing research, GMMs continue to unlock insights from complex datasets.

How interested are you in uncovering even more about this topic? Our next article dives deeper into [insert next topic], unravelling insights you won’t want to miss. Stay curious and take the next step with us!