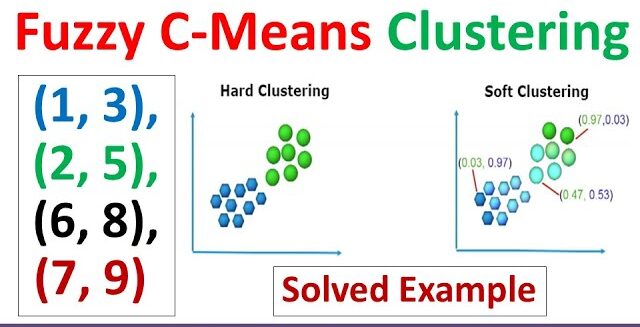
A Brief History: Who Developed It?
Fuzzy C-means (FCM), also known as fuzzy clustering, was introduced in 1973 by James C. Bezdek. It transformed clustering analysis by allowing data points to belong to multiple clusters. Building on the foundations of clustering and fuzzy logic, FCM became a go-to technique in fields such as pattern recognition, machine learning, and image processing.
What Is Fuzzy C-Means?
Imagine organising a closet. Some items, like a sweater, clearly belong in the “winter wear” pile, but a light jacket might fit into both “winter wear” and “spring wear.” Fuzzy C-means reflects this flexibility: it assigns data points to multiple clusters with varying membership levels, making it ideal for complex datasets.
Why Is It Used? What Challenges Does It Address?
Fuzzy C-means tackles key clustering challenges:
- Overlapping Clusters: Models real-world data where points naturally belong to multiple groups.
- Flexible Membership: Assigns probabilities to reflect the likelihood of belonging to each cluster.
- Improved Decision-Making: Provides clarity in complex datasets with overlapping features.
Without FCM, traditional clustering techniques often oversimplify nuanced datasets, leading to inaccurate results.
How Is Fuzzy C-Means Used?
Fuzzy C-means is implemented through the following steps:
- Initialisation: Define the initial cluster centres.
- Membership Calculation: Compute membership values for data points relative to each cluster.
- Iteration: Refine clusters and memberships iteratively until convergence.
This process outputs clusters with probability scores, offering a clear view of data point associations. Tools like Scikit-fuzzy (Python) and MATLAB simplify implementation for both beginners and professionals.
Specialised Types of Fuzzy C-Means
Fuzzy C-means adapts to different datasets through specialised variations:
- Kernel-Based Fuzzy C-Means: Handles non-linear data with kernel functions.
- Weighted Fuzzy C-Means: Adjusts for feature importance with weighted metrics.
These variants enhance FCM’s versatility across diverse datasets.
Key Features of Fuzzy C-Means
Fuzzy C-means is defined by several notable features:
- Membership Probabilities: Quantify how strongly a point belongs to each cluster.
- Fuzzification Factor: Customisable for finer control of cluster assignments.
- Robust Noise Handling: Effectively accommodates noise and ambiguity in data.
Popular Tools for Fuzzy C-Means
Several tools make Fuzzy C-means accessible for researchers and analysts:
- Scikit-fuzzy (Python): A specialised library for fuzzy clustering applications.
- MATLAB: Offers an intuitive toolbox for FCM and its variations.
- R Libraries: Packages like e1071 provide user-friendly functions for fuzzy clustering.
Applications of Fuzzy C-Means in Australian Governmental Agencies
Fuzzy C-means has practical applications across various Australian government sectors:
- Healthcare Analytics:
- Application: Segmenting patient demographics for personalised healthcare strategies.
- Use of FCM: Groups patients based on health metrics, enabling targeted interventions.
- Environmental Modelling:
- Application: Clustering weather patterns for precise climate projections.
- Use of FCM: Improves the accuracy of environmental forecasts and resource management.
- Education Policy Development:
- Application: Identifying student performance clusters to design targeted support programmes.
- Use of FCM: Enables the development of customised strategies to enhance student outcomes.
Conclusion
Fuzzy C-means (FCM) is a versatile and powerful clustering technique that addresses the complexities of real-world datasets by allowing overlapping clusters and probabilistic memberships. Its flexibility, supported by robust tools and software, makes it indispensable in fields ranging from healthcare to environmental modelling and education policy development.
How interested are you in uncovering even more about this topic? Our next article dives deeper into [insert next topic], unravelling insights you won’t want to miss. Stay curious and take the next step with us!