A Brief History of This Tool
Bayesian Networks, introduced by Judea Pearl in the 1980s, revolutionized the modeling of uncertainty in complex systems: his work integrated probability theory and graph theory to address challenges in reasoning under uncertainty. This tool has become a cornerstone in artificial intelligence, decision-making, and machine learning, enabling precise modeling of cause-effect relationships.
What Is It?
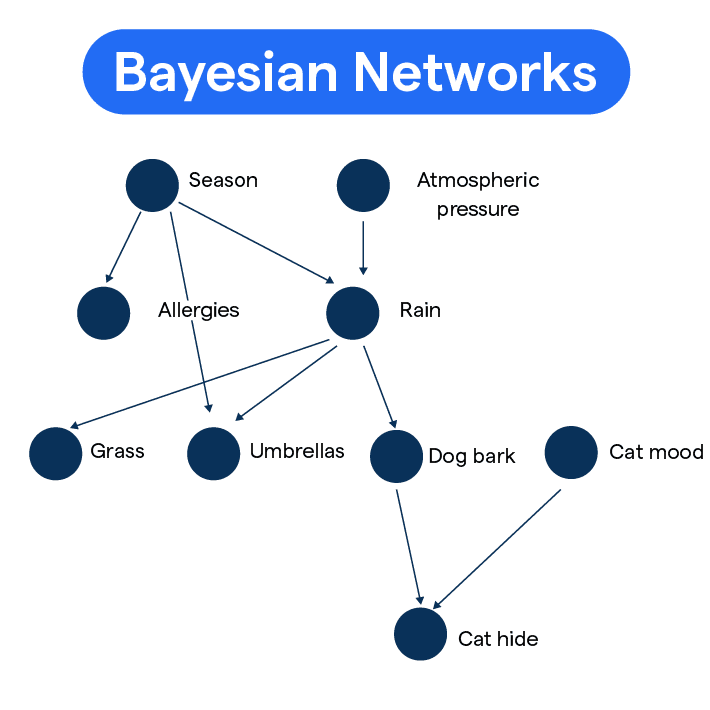
A Bayesian Network is a probabilistic graphical model that represents variables and their conditional dependencies using a directed acyclic graph (DAG). Nodes in the graph symbolize variables, while edges represent causal or probabilistic relationships, quantified through conditional probability tables (CPTs).
Imagine a Bayesian Network as a roadmap where intersections (nodes) are variables, and roads (edges) connect them based on relationships. Just as traffic at one intersection can influence another, changes in one variable affect others in the network.

Why It Is Being Used? What Challenges Are Being Addressed?
Bayesian Networks solve problems related to decision-making under uncertainty:
- Complex Dependencies: They model intricate relationships in systems like healthcare diagnostics and predictive maintenance.
- Causal Reasoning: They uncover and quantify cause-effect relationships.
- Uncertainty Management: They estimate probabilities for various outcomes, even with incomplete or noisy data.
How It Is Being Used?
- Define Variables: Identify key variables and relationships.
- Construct the Graph: Build a directed acyclic graph (DAG) to depict dependencies.
- Quantify Probabilities: Use conditional probability tables (CPTs) for each node.
- Perform Inference: Apply algorithms to compute probabilities for decision-making and predictions.
Different Types
- Static Bayesian Networks: Model systems without time dependency.
- Dynamic Bayesian Networks (DBNs): Extend Bayesian Networks to include time-series analysis.
Different Features
- Visual Representation: Simplifies complex relationships into an interpretable graphical structure.
- Causal Analysis: Supports discovery and quantification of cause-effect dynamics.
- Adaptability: Dynamically incorporates new evidence for real-time predictions.
Different Software and Tools for It
- GeNIe: A tool for building and analyzing Bayesian Networks with a user-friendly interface.
- PyMC3: A Python library for probabilistic programming.
- bnlearn: An R package for learning and visualizing Bayesian Networks.
- TensorFlow Probability: Integrates Bayesian Networks with deep learning frameworks.
Three Industry Application Examples in Australian Governmental Agencies
- Department of Health: Models disease progression and optimizes healthcare resource allocation.
- Australian Bureau of Statistics: Uses Bayesian Networks to analyze demographic trends and predict social outcomes.
- Australian Border Force: Enhances risk assessment by detecting anomalies in trade and customs data.
How interested are you in uncovering even more about this topic? Our next article dives deeper into [insert next topic], unravelling insights you won’t want to miss. Stay curious and take the next step with us!