A Very Short Introduction of Lasso Regularization in Machine Learning

A Brief History: Who Developed Lasso Regularization?

Lasso regularization, also known as Least Absolute Shrinkage and Selection Operator, was introduced by Robert Tibshirani in 1996 to address the challenges of feature selection and overfitting in regression models. Developed within the field of statistics, it has since become a cornerstone in machine learning workflows, especially for high-dimensional datasets where the number of features often exceeds the number of observations.

What Is Lasso Regularization?

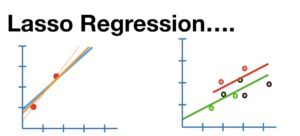
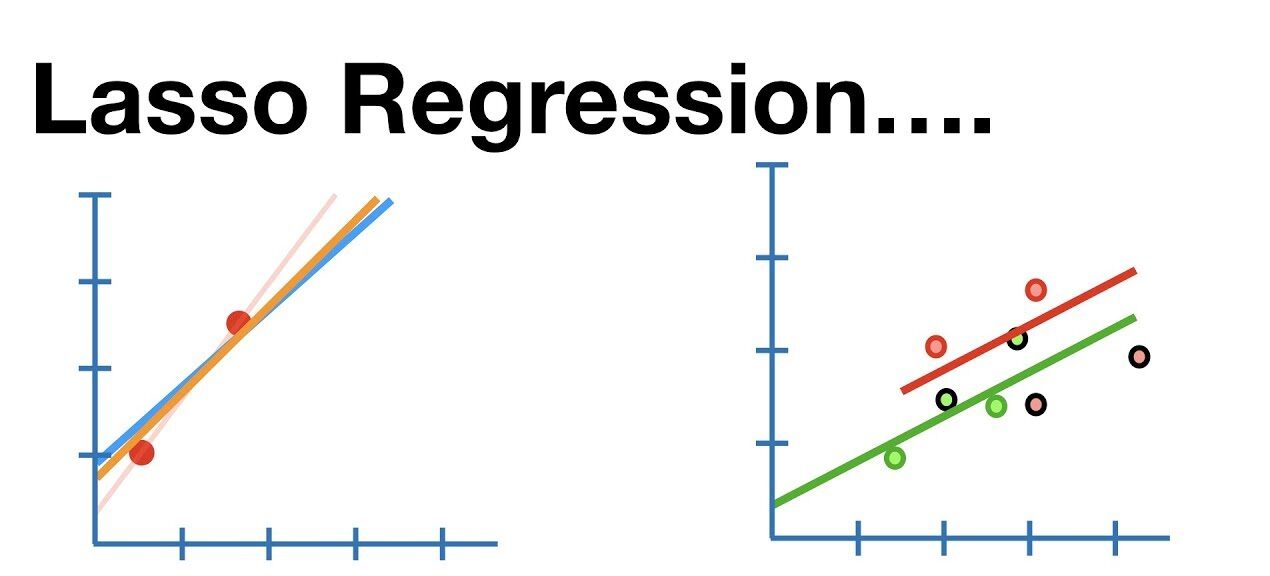
Lasso regularization is a technique that helps models focus on the most important predictors by penalizing large coefficients. By introducing a penalty proportional to the absolute values of the coefficients, it effectively forces irrelevant features to shrink to zero. This approach allows models to prioritize the most meaningful features while ignoring unnecessary noise, much like pruning overgrown branches in a garden to help healthy plants thrive.

Why Is It Used? What Challenges Does It Address?

Lasso regularization tackles critical challenges in machine learning models:

• Feature Selection: Automatically eliminates irrelevant or redundant features by shrinking their coefficients to zero.
• Overfitting Prevention: Reduces model complexity, ensuring better generalization on unseen data.
• Improved Interpretability: Simplifies models by focusing on key predictors, making results easier to understand and apply.

Without Lasso regularization, models processing high-dimensional data may become overly complex, leading to poor performance on real-world applications.

How Is It Used?

1. Add a Lasso Penalty: Include an L1 penalty term in the model’s loss function.
2. Set the Regularization Parameter (Alpha): Adjust alpha to control the strength of the penalty.
3. Optimize the Model: Use gradient descent or other optimization methods to minimize the loss function, balancing accuracy and feature selection.

Different Types

• Standard Lasso Regression: Applies L1 regularization to perform feature selection in regression tasks.
• Elastic Net Regularization: Combines Lasso (L1) and Ridge (L2) penalties, balancing feature selection with coefficient stability.

Key Features

• Automatic Feature Selection: Shrinks irrelevant coefficients to zero, simplifying the model.
• Model Simplicity: Produces sparse, interpretable models suitable for decision-making.
• Versatility: Works effectively for linear regression models, classification tasks, and high-dimensional datasets.

Software and Tools Supporting Lasso Regularization

• Python Libraries:
  • Scikit-learn: Offers built-in support for Lasso regression with hyperparameter tuning for alpha.
  • TensorFlowand PyTorch: Allow custom implementations of L1 regularization in deep learning models.
  • XGBoostand LightGBM: Integrate L1 penalties within their gradient boosting frameworks.
• Platforms: Google Colab and Jupyter Notebooks provide flexible environments for implementation and visualization.

3 Industry Application Examples in Australian Governmental Agencies

1. Healthcare (Department of Health):
   • Application: Predicting patient outcomes from diagnostic data.
   • Use of Lasso Regularization: Focuses on the most relevant medical features, excluding redundant or irrelevant test results.
2. Environmental Management (Department of Agriculture, Water, and the Environment):
   • Application: Modeling the relationship between environmental factors and biodiversity.
   • Use of Lasso Regularization: Identifies key predictors like rainfall and temperature, ignoring noise in complex datasets.
3. Education (Department of Education):
   • Application: Analyzing factors influencing student performance in standardized testing.
   • Use of Lasso Regularization: Highlights critical predictors such as attendance and socio-economic status while eliminating less impactful data.