A Very Short Introduction of Ridge Regularization

A Brief History: Who Developed Ridge Regularization?

Ridge regularization, also known as L2 regularization, emerged in the 1970s to address multicollinearity in linear regression models. Researchers Arthur E. Hoerl and Robert W. Kennard pioneered this technique to stabilize regression models and improve their predictive accuracy. It has since become a cornerstone in machine learning workflows, particularly for overfitting prevention and generalization improvement.

What Is Ridge Regularization?

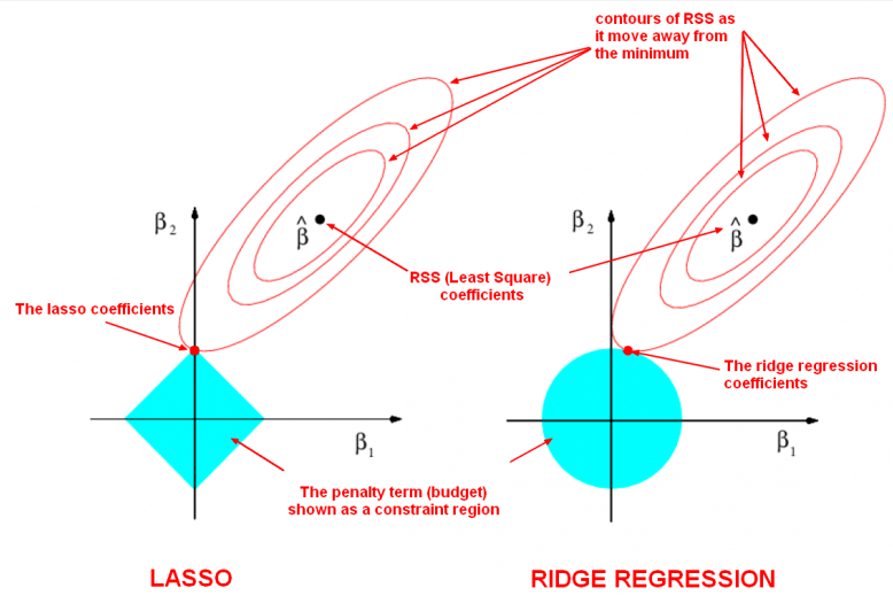
Ridge regularization reduces overfitting by introducing a penalty term proportional to the square of the coefficients. This discourages large weights, ensuring the model generalizes well to unseen data.Ridge regularization is like using shock absorbers in a car. On bumpy roads (datasets with noise or multicollinearity), the absorbers smooth the ride (predictions), ensuring stability and reliability.

Why Is It Used? What Challenges Does It Address?

Ridge regularization addresses several critical challenges in machine learning:

• Preventing Overfitting: Reduces the risk of memorizing noise in the data.
• Improving Model Stability: Handles multicollinearity by shrinking correlated feature coefficients.
• Enhancing Generalization: Boosts prediction accuracy on real-world datasets.

Without Ridge regularization, models with small datasets or highly correlated features risk overfitting, leading to unreliable performance in real-world applications.

How Is It Used?

1. Introduce a Ridge Penalty: Add the L2 penalty term to the model’s loss function.
2. Set a Regularization Parameter (Alpha): Tune the weight of the penalty to balance coefficient shrinkage and error minimization.
3. Optimize the Model: Minimize the modified loss function using gradient descent algorithms or other optimization techniques.

Different Types

• Standard Ridge Regression: The traditional application of L2 regularization in regression analysis.
• Elastic Net Regularization: A hybrid approach combining Ridge (L2) and Lasso (L1) regularization for balancing feature selection and model stability

Key Features

• Smooth Coefficient Shrinkage: Prevents large weight values while retaining all features.
• Stability: Mitigates the impact of multicollinearity for more consistent predictions.
• Flexibility: Works well for linear regression models and classification algorithms.

Software and Tools Supporting Ridge Regularization

• Python Libraries:
  • Scikit-learn: Provides Ridge regression with tools for hyperparameter tuning.
  • TensorFlowand PyTorch: Enable custom implementations of Ridge regularization in deep learning models.
  • XGBoostand LightGBM: Offer built-in L2 regularization for gradient boosting.
• Platforms: Google Colab and Jupyter Notebooks for accessible implementation and visualization.

3 Industry Application Examples in Australian Governmental Agencies

1. Healthcare (Department of Health):
   • Application: Predicting patient recovery rates from diagnostic data.
   • Use of Ridge Regularization: Improves model reliability by controlling the influence of correlated medical features, such as overlapping test results.
2. Environmental Management (Department of Agriculture, Water, and the Environment):
   • Application: Forecasting water availability in drought-prone regions.
   • Use of Ridge Regularization: Provides robust predictions by managing correlations in environmental data.
3. Transportation (Department of Infrastructure, Transport, and Regional Development):
   • Application: Predicting urban traffic patterns based on sensor data.
   • Use of Ridge Regularization: Enhances stability and accuracy when analyzing highly correlated traffic indicators.