A Brief History of This Tool
The Metropolis-Hastings algorithm, a cornerstone of Bayesian computation, began its journey in 1953 with Nicholas Metropolis and gained further refinement in 1970 through W.K. Hastings. Initially devised for thermodynamic simulations, this algorithm has since expanded its utility to fields like machine learning, genomics, and environmental science. It provided an efficient and practical way to sample from complex probability distributions, revolutionizing computational statistics.
What Is It?
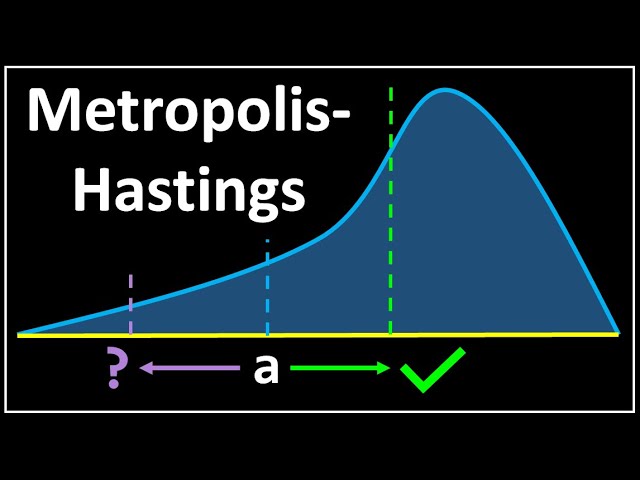
Metropolis-Hastings is a Markov Chain Monte Carlo (MCMC) algorithm designed to generate samples from intricate probability distributions. The process is iterative: it proposes potential samples and uses a probability rule to decide whether to accept or reject them.
Imagine navigating a mountain trail with a flashlight. The flashlight represents the probability function, revealing small sections of the trail. Each step you take—whether forward, backward, or to the side—is guided by the flashlight’s beam. Over time, your careful navigation builds a detailed map of the mountain (the probability distribution), one step at a time.
Why Is It Being Used? What Challenges Are Being Addressed?
Metropolis-Hastings tackles key challenges in probabilistic modeling, including:
- Efficient Sampling: Allows exploration of high-dimensional probability distributions that are computationally expensive to analyze.
- Bayesian Inference: Provides estimates of posterior distributions for models with complex structures.
- Flexibility: Accommodates a variety of applications, from optimization to parameter estimation, thanks to its adaptable design.
How Is It Being Used?
- Define the Target Distribution: Specify the probability distribution you aim to sample.
- Choose a Proposal Distribution: Use a simpler model to propose new samples.
- Apply the Acceptance Rule: Evaluate proposed samples and decide to include or discard them based on a calculated acceptance ratio.
- Iterate: Repeat the process to construct a chain of samples that approximate the target distribution.
Different Types of Metropolis-Hastings Sampling
- Symmetric Metropolis Algorithm: Proposes samples with equal forward and backward probabilities.
- Random-Walk Metropolis-Hastings: Proposes samples using a Gaussian distribution centered at the current state.
- Adaptive Metropolis-Hastings: Dynamically adjusts the proposal distribution to improve sampling efficiency.
Different Features of Metropolis-Hastings Sampling
- Iterative Refinement: Improves accuracy as the algorithm progresses through more iterations.
- Scalable Design: Handles high-dimensional probability distributions effectively.
- Customizable Proposals: Adapts to domain-specific needs through tailored proposal distributions.
Different Software and Tools for It
- Stan: A leading probabilistic programming language for Bayesian modeling.
- PyMC3: A Python library designed for MCMC algorithms, including Metropolis-Hastings.
- R (mcmc package): Offers simulation tools for Markov Chains.
- MATLAB: Includes built-in functions for MCMC techniques like Metropolis-Hastings.
Three Industry Application Examples in Australian Governmental Agencies
- Australian Bureau of Statistics: Uses Metropolis-Hastings for estimating missing values and refining population models.
- CSIRO: Applies it in environmental modeling to predict climate variability and assess risks.
- Australian Energy Market Operator (AEMO): Employs it to optimize energy demand forecasting and enhance grid reliability.
