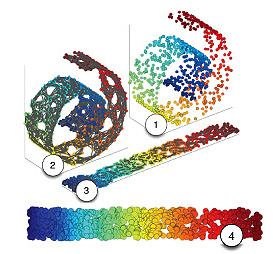
What Is Manifold Learning? Simplifying Complex Data
Manifold learning is a class of unsupervised machine learning algorithms designed to simplify high-dimensional data into low-dimensional representations while retaining meaningful data structures. Techniques like Isomap, Locally Linear Embedding (LLE), and t-SNE have revolutionised how we process and visualise complex datasets.

Why Use Manifold Learning? Solving Data Challenges
Manifold learning addresses challenges in analysing datasets with numerous features, where traditional methods like Principal Component Analysis (PCA) fail to capture nonlinear patterns. Its key applications include:
- Data Visualisation: Simplifies complex datasets for exploration and communication.
- Dimensionality Reduction: Reduces computational costs for downstream tasks.
- Pattern Recognition: Identifies clusters, relationships, and hidden structures in data.
How Manifold Learning Works: A Step-by-Step Guide
Manifold learning algorithms follow these steps:
- Representing data points as nodes in a graph structure.
- Calculating pairwise distances or similarities between nodes.
- Embedding the graph into a low-dimensional space while preserving structural integrity.
Popular Manifold Learning Techniques: Isomap, LLE, and t-SNE
Manifold learning methods vary based on their approach to data representation:
- Isomap: Preserves global structures by using geodesic distances on a neighbourhood graph.
- Locally Linear Embedding (LLE): Maintains local relationships through linear approximations.
- Laplacian Spectral Embedding: Utilises spectral graph theory for smooth, low-dimensional mappings.
- t-SNE: Optimises embeddings by minimising divergence between high-dimensional and low-dimensional data distributions.
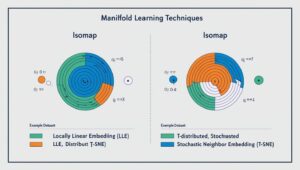
Key Features of Manifold Learning Algorithms
Manifold learning stands out for its:
- Nonlinear Adaptability: Captures intricate data relationships missed by linear methods.
- Scalable Performance: Efficiently handles large datasets.
- Multi-Domain Flexibility: Effective across text, image, and biological data analysis.
Top Tools for Manifold Learning: Scikit-Learn, UMAP, and More
Manifold learning is supported by several tools and libraries:
- Scikit-learn: Implements popular methods like Isomap and LLE.
- Matplotlib + t-SNE: Provides visualisations for t-SNE embeddings.
- UMAP: A robust alternative for dimensionality reduction with scalable performance.
- PyTorch Geometric: Supports advanced graph-based learning frameworks for complex datasets.
Manifold Learning in Action: Australian Government Applications
Manifold learning is already driving impactful results in Australia:
- Department of Education: Uses t-SNE to analyse student performance data, identifying clusters and trends for targeted interventions.
- Australian Bureau of Statistics: Leverages Isomap to visualise demographic distributions effectively.
- CSIRO: Applies Laplacian spectral embedding to genomic data, improving agricultural research outcomes.
How interested are you in uncovering even more about this topic? Our next article dives deeper into [insert next topic], unravelling insights you won’t want to miss. Stay curious and take the next step with us!